4486. Cheburashka and Crocodile Gena

When Cheburashka and Crocodile Gena don’t know what to do, they play various interesting games. Today, Gena came up with a new game that, in his opinion, will help Cheburashka improve his arithmetic skills.

The rules of the game are simple: Gena takes n wooden boards, numbers them from 1 to n, and writes some numbers on them. Then, he announces two numbers l and r, and Cheburashka must calculate the sum of all numbers on the boards numbered from l to r.

To prevent Cheburashka from memorizing all possible answers, Gena occasionally modifies the numbers. Specifically, he replaces all numbers in the range [l, r] with a sequence of numbers from 1 to r – l + 1 in ascending order.

Cheburashka is not very good at arithmetic yet, so he asks you to write a program to help him perform these calculations.

Input. The first line contains one integer n (1 ≤ n ≤ 10⁶) – the number of boards.

The second line contains n integers – the initial values written on the boards (each number does not exceed 10⁹).

The third line contains an integer m (1 ≤ m ≤ 10⁵) – the number of queries.

The next m lines each describe one of two types of queries. The first number in each line, t (1 ≤ t ≤ 2), indicates the type of query:

· If t = 1, it is followed by two numbers l and r. You need to compute the sum of all numbers on the boards numbered from l to r.

· If t = 2, it is followed by two numbers l and r. This means that the numbers on the boards numbered from l to r are replaced with the sequence 1, 2, … , r – l + 1.

It is guaranteed that all queries are valid, and board numbering starts from 1.

Output. For each query of type 1, print one number – the sum of values on the boards in the given range [l, r].

Sample input

Sample output

5 3 2 4 5

1 1 5

1 2 3

2 1 5

2 2 5

1 1 5

SOLUTION

data structures – segment tree

Algorithm analysis

Let’s construct a segment tree that supports a summation operation. In each node (representing a fundamental segment [a; b]), we’ll additionally store a value left. If left > 0, it means there is a pending operation in the segment [a; b]: all nodes in its subtree should be assigned values left, left + 1, …, left + b – a. Initially, left is set to zero in all nodes.

Now, let’s consider the process of propagating values. Suppose a query q(x, y) partially overlaps both subtrees, meaning x ≤ m < y. In this case:

· For the left child, set left = 1.

· For the right child, set left to 1 plus the length of the segment [x; m].

If a ≠ x (b ≠ y), the left value should be propagated further.

If x ≥ m + 1 (meaning the query segment lies entirely in the right subtree), then the left value for the left child remains 0.

Now, consider a query q(x, y) that is covered by a set of fundamental segments [a₁, b₁], [a₂, b₂], …, [a_k, b_k]. In this case, assign the left value for segment [a_i, b_i] as:

1 + sum of lengths of all previous segments [a_j, b_j], for which j < i

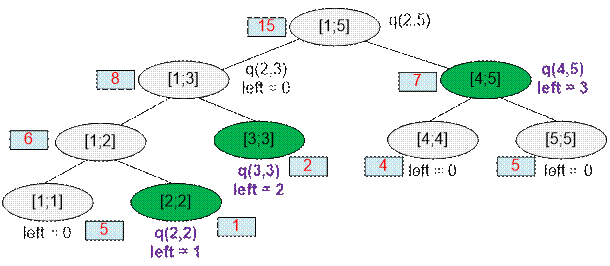
For example, suppose the segment tree is built for the range [1, 8], and the query q(2, 7) covers the following fundamental segments:

Example

Let’s consider the following test:

5 3 2 4 5

2 2 5

1 1 3

Next to each node in the rectangle, the sum over the segment is written.

Algorithm implementation

Declare the array SegTree to store the segment tree.

struct node

{

long long summa;

int left;

};

vector<node> SegTree;

The function BuildTree constructs the segment tree.

void BuildTree(int v, int lpos, int rpos)

{

if (lpos == rpos)

SegTree[v].sum = a[lpos];

else

{

int mid = (lpos + rpos) / 2;

BuildTree(2 * v, lpos, mid);

BuildTree(2 * v + 1, mid + 1, rpos);

SegTree[v].sum = SegTree[2 * v].sum + SegTree[2 * v + 1].sum;

}

The function Sum computes the sum of numbers from a to b.

long long Sum(int a, int b)

{

return 1LL * (a + b) * (b - a + 1) / 2;

}

The function Push propagates the left value from node v to its children. The sum sum in the child nodes is then recomputed.

void Push(int v, int lpos, int mid, int rpos)

{

if (SegTree[v].left)

{

SegTree[2 * v].left = SegTree[v].left;

SegTree[2 * v].sum = Sum(SegTree[2 * v].left,

SegTree[2 * v].left + mid - lpos);

SegTree[2 * v + 1].left = SegTree[v].left + mid - lpos + 1;

SegTree[2 * v + 1].sum = Sum(SegTree[2 * v + 1].left,

SegTree[2 * v + 1].left + rpos - mid - 1);

SegTree[v].left = 0;

}

The function Update fills the range [left; right] with the sequence of values from, from + 1, from + 2, ….

void Update(int v, int lpos, int rpos, int left, int right, int from)

{

if (left > right) return;

if ((lpos == left) && (rpos == right))

{

SegTree[v].left = from;

SegTree[v].sum = Sum(from, from + right - left);

return;

}

int mid = (lpos + rpos) / 2;

int midval = mid - left + 1;

If the query segment [left; right] lies entirely within the right subtree [mid + 1; rpos], pass the value from to the right child without changes (while setting midval to zero).

if (midval < 0) midval = 0;

Push(v, lpos, mid, rpos);

Update(2 * v, lpos, mid, left, min(mid, right), from);

Update(2 * v + 1, mid + 1, rpos, max(left, mid + 1),

right, from + midval);

SegTree[v].sum = SegTree[2 * v].sum + SegTree[2 * v + 1].sum;

}

The function Summa returns the sum of numbers in the range [left; right].

long long Summa(int v, int lpos, int rpos, int Left, int Right)

{

if (Left > Right) return 0;

if ((lpos == Left) && (rpos == Right)) return SegTree[v].sum;

int mid = (lpos + rpos) / 2;

Push(v, lpos, mid, rpos);

return Summa(2 * v, lpos, mid, Left, min(mid, Right)) +

Summa(2 * v + 1, mid + 1, rpos, max(Left, mid + 1), Right);

}

The main part of the program. Read the input array of numbers.

scanf("%d", &n);

a.resize(n + 1);

for(i = 1; i <= n; ++i)

scanf("%d", &a[i]);

Construct the segment tree.

SegTree.resize(4 * n);

BuildTree(1, 1, n);

Sequentially process q queries.

scanf("%d", &q);

for(i = 0; i < q; ++i)

{

scanf("%d %d %d", &type, &l, &r);

if(type == 1)

printf("%lld\n", Summa(1,1,n,l,r));

else

Update(1,1,n,l,r,1);

}